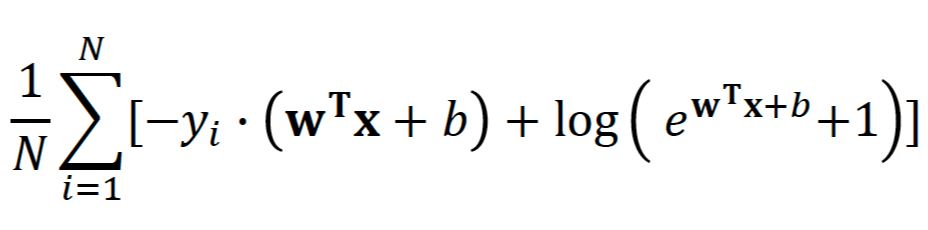Logistic Regression

대학교 공부/기계학습

Logistic Regression

유태정 2022. 12. 13. 16:35

OpenAI Chat에서 인용

Regression

회귀 분석은 종속 변수와 하나 이상의 독립 변수 사이의 관계를 모형화하는 데 사용되는 통계적 방법입니다. 독립 변수의 값을 기반으로 종속 변수의 값을 예측하는 데 사용됩니다. 회귀 분석에서 선 또는 곡선은 종속 변수의 관측된 값과 모형에서 예측한 값 사이의 차이를 최소화하는 방식으로 데이터에 적합됩니다. 데이터에 적합한 선 또는 원곡선을 회귀선 또는 회귀 곡선이라고 합니다. 회귀 분석의 목표는 독립 변수의 값을 기반으로 종속 변수를 예측하는 데 사용할 수 있는 가장 적합한 선 또는 곡선을 찾는 것입니다.

Logistic Regression

로지스틱 회귀 분석은 하나 이상의 독립 변수를 기반으로 이항 종속 변수(즉, 두 값만 가질 수 있는 변수)의 결과를 예측하는 데 사용되는 통계 모형화의 한 유형입니다. 이러한 유형의 회귀 분석은 로지스틱 함수를 사용하여 주어진 예제가 가능한 두 클래스 중 하나에 속할 확률을 모형화하기 때문에 "로지스틱"이라고 합니다. 로지스틱 함수는 실수 값을 0과 1 사이의 값에 매핑하므로 확률 모형화에 유용한 함수입니다. 로지스틱 회귀 분석에서는 예측 확률을 사용하여 종속 변수를 예측합니다. 예를 들어, 주어진 예제가 양의 클래스에 속할 것이라는 예측 확률이 0.5보다 크면 모형은 예제가 양의 클래스에 속할 것이라고 예측합니다.

Sigmoid Function

시그모이드 함수는 기계 학습 및 인공 신경망에서 일반적으로 사용되는 수학 함수입니다. 실제 값 입력을 가져와서 0과 1 사이의 값에 매핑하는 활성화 함수의 일종입니다. 이 함수는 확률을 모델링하는 데 유용하며, 예제가 두 클래스 중 하나에 속할 확률을 예측하는 것이 목표인 이진 분류 문제에서 종종 사용됩니다. 시그모이드 함수는 다음과 같이 정의됩니다.

f(x) = 1 / (1 + e^(-x))

여기서 x는 입력 값이고 e는 자연 로그의 기저값입니다. 시그모이드 함수는 S자형 곡선을 가지며, 로지스틱 함수를 사용하여 확률을 모형화하기 때문에 로지스틱 함수라고 불리기도 합니다. 시그모이드 함수는 미분 가능하므로 그레이디언트 기반 최적화 알고리듬을 사용하여 기계 학습 모델을 훈련하는 데 유용합니다.

Training Logistic Regression

로지스틱 회귀 분석 모형을 학습하려면 다음 단계를 수행해야 합니다.

학습 데이터 수집 및 준비: 첫 번째 단계는 모델을 교육하는 데 사용될 학습 데이터를 수집하고 준비하는 것입니다. 여기에는 일반적으로 관련 특징(예: 독립 변수)과 대상 변수(예: 종속 변수)를 선택하고 Missing Variables, Outliers 및 기타 데이터 문제를 제거하기 위해 데이터를 전처리하는 작업이 포함됩니다.
손실 함수 선택: 다음 단계는 학습 중에 모델의 정확도를 측정하는 데 사용할 손실 함수(비용 함수라고도 함)를 선택하는 것입니다. 로지스틱 회귀 분석에 가장 일반적으로 사용되는 손실 함수는 예측 확률과 실제 확률 간의 차이를 측정하는 the binary cross-entropy loss입니다.
최적화 알고리즘 선택: 손실 함수를 선택했으면 다음 단계는 손실 함수를 최소화하는 데 사용할 최적화 알고리즘을 선택하고 가장 적합한 모델을 찾는 것입니다. 로지스틱 회귀 분석에 가장 일반적으로 사용되는 최적화 알고리듬은 확률적 경사 하강법(SGD)으로, 모델 가중치에 대한 손실 함수의 기울기를 기반으로 모델 가중치를 반복적으로 업데이트합니다.
모델 학습: 최적화 알고리듬을 선택한 후에는 훈련 데이터를 제공하고 최적화 알고리듬을 사용하여 손실 함수를 최소화하고 가장 적합한 모델을 찾아 모델을 훈련할 수 있습니다. 여기에는 일반적으로 교육 데이터를 여러 번 반복하고 각 반복에서 모델 가중치를 조정하는 작업이 포함됩니다.
모델 평가: 모델을 교육한 후 새로운 데이터에 대한 성능을 평가하여 새로운 예제로 얼마나 잘 일반화되는지 확인하는 것이 중요합니다. 이 작업은 훈련된 모델을 사용하여 보류된 테스트 세트에 대한 예측을 수행하고 예측을 대상 변수의 실제 값과 비교하여 수행할 수 있습니다. 로지스틱 회귀 분석 모형을 평가하는 데 사용되는 가장 일반적인 메트릭은 정확도, 정밀도, 리콜 및 F1 점수입니다.
모델 미세 조정: 모델을 훈련하고 평가한 후에는 성능을 향상시키기 위해 모델 하이퍼 파라미터(예: 학습 속도, 정규화 강도 등)를 조정하여 모델을 미세 조정해야 할 수 있습니다. 여기에는 일반적으로 서로 다른 하이퍼 파라미터 값을 사용하여 여러 버전의 모델을 교육하고 검증 세트에서 가장 잘 수행되는 모델을 선택하는 작업이 포함됩니다.

✓ 손실함수로 평균제곱오차(MSE; Mean Squared Error)는 사용하지 않는다. Sigmoid Function에 이를 적용하면 그래프가 무척 굴곡지게 나타나게 된다. 그러면 경사하강법을 적용했을 때 적합한 최적화 지점을 찾기 힘들어지게 된다. 그래서 우리는 (위에서 소개한 것과 같이) Log Loss(the Binay Cross-Entropy Loss)를 채택한다.

Log Loss

Log Loss 함수는 이진 분류 작업에서 일반적으로 사용되는 손실 함수이며, 여기서 목표는 예제가 두 클래스 중 하나에 속할 확률을 예측하는 것입니다. 예측 확률의 로그를 사용하여 손실을 계산하기 때문에 "Log Loss"이라고 합니다. Log Loss 함수는 다음과 같이 정의됩니다.

Log Loss = -y * log(p) - (1 - y) * log(1 - p)

여기서 y는 참 레이블(0 또는 1)이고 p는 양의 클래스의 예측 확률(즉, 예제가 양의 클래스에 속할 확률)입니다. Log Loss 함수는 예측 확률과 실제 확률 간의 차이를 나타내는 측도입니다. Log Loss가 작으면 예측 확률이 실제 확률에 가깝다는 것을 나타내며, Log Loss가 크면 예측 확률이 실제 확률과 거리가 멀다는 것을 나타냅니다.

✓ Log Loss 함수는 입력 데이터 하나에 대해서만 값을 계산해준다. 하지만 우리는 전체 데이터에 대한 값으로 모델 파라미터를 예측해야 한다. 따라서 목적함수를 정의해야 하는데, 이는 모든 데이터에 대한 Log Loss의 평균으로 나타내어진다. 이를 잘 정리하면 아래 식이 된다.